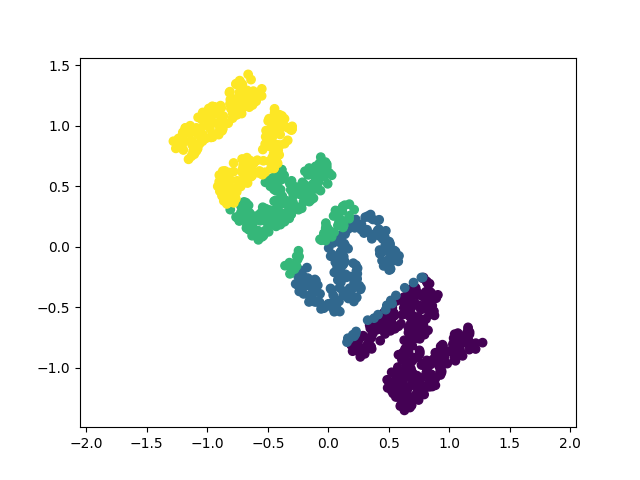
また距離行列は任意の次元データから計算できます。例えば、2次元平面上のデータを3次元に投影します。
MDS推定器にこの3次元データを入力して距離行列を計算した後、この距離行列の最適な2次元埋め込みを決定することができます。その結果、もとのデータ表現が復元されます。
先ほどのコードでrandom_projection()関数を実行すると以下のようなグラフができます。
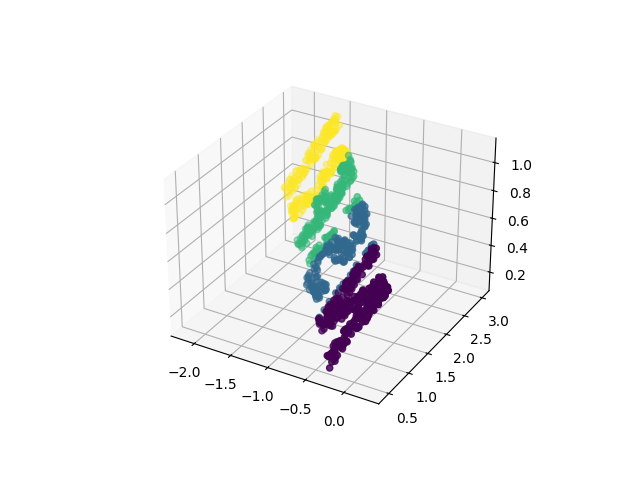
このような3次元データを元の2次元に復元することが、多様体学習推定器の本質的な目的です。高次元の埋め込みデータを与えると、データ内の特定の関係を保持する低次元のデータ表現を求めます。MDSの場合、保存される量は全てのポイント間の距離です。
先ほどのコードに以下のコードを追加して、加工します。
model=MDS(n_components=2,random_state=1701)
X4=model.fit_transform(X3)
plt.scatter(X4[:,0],X4[:,1],**colorize)
plt.axis('equal');
これを実行すると以下のような2次元の復元画像を得ることができます。